Forskjell mellom tre og graf i datastruktur | Trær vs Graf i datastruktur
Tror vs graf i datastruktur
Siden trær og graf er de ikke-lineære datastrukturene som brukes til å løse komplekse dataproblemer, og vet at forskjellen mellom tre og graf i datastruktur er nyttig. Begge datastrukturene representerer dataelementene i matematisk form. Hovedformålet med artikkelen er å markere betydningen av ikke-lineære datastrukturer. Det inkluderer også nøkkelforskjell mellom disse to datastrukturene.
Hva er et tre i datastruktur?
Trær er en ikke-lineær datastruktur der alle dataposter er arrangert i noen sorterte sekvenser. Trær definerer et begrenset sett med dataposter. Hvert datapunkt betegnes som noden. Det er en spesiell foreldre node som også kalles rotnoden. Alle andre noder er barneknuter eller underbarn noder. Hovedformålet med treet er å representere hierarkisk forhold mellom ulike dataposter. Normalt tre vokser i øvre retning, men datastruktur tree vokser i ned retning. Alle undernoder knyttet til treet er delt inn i ulike nivåer. Binært tre er det vanligste eksempelet på ikke-lineær datastruktur. Maksimal grad av et binært tre er to. Det betyr at maksimalt to noder kan festes med hver foreldre node.

Hva er graf i datastruktur?
Graf er en populær ikke-lineær datastruktur som brukes til å løse ulike dataproblemer. De er vant til å designe ulike spill og puslespill. Grafer kan deles inn i mange kategorier. Disse er:
• Regissert graf: I den rettede grafen defineres hver kant av bestilt par punkter.
• Ikke-rettet graf: I den ikke-rettede grafen er hver kant definert av uordnet par krysser
• Tilkoblet graf: I den tilkoblede banen er det en sti fra hvert toppunkt til hvert annet toppunkt.
• Ikke-koblet graf: I den ikke-tilkoblede grafen eksisterer ikke banen fra et vertex til et annet vertex.
• Vektet graf: I vektet graf er det lagt vekt på kanten.
• Enkel graf eller Multi Graph
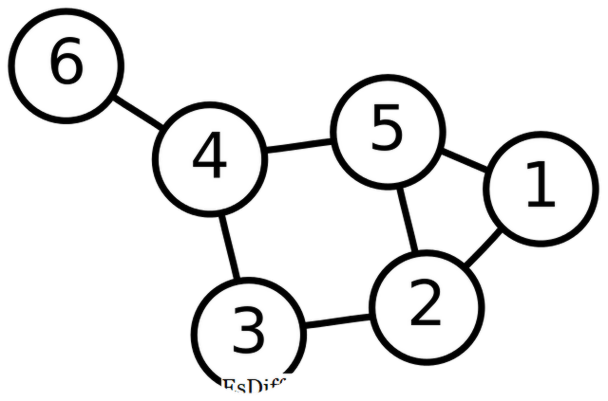
Likheter mellom Tree og Graph i datastruktur
• Trær og graf begge deler er ikke-lineær datastruktur som brukes til å løse komplekse datamaskiner problemer.
• Begge datastrukturene bruker en overordnet node og flere undernoder.
Hva er forskjellen mellom Tree og Graph i datastruktur?
• Trær regnes som et spesielt tilfelle av graf.Det kalles også som en minimal koblet graf.
• Hvert tre kan betraktes som en graf, men hver graf kan ikke betraktes som et tre.
• Selvløkker og kretser er ikke tilgjengelige i treet som i tilfelle av grafer.
• For å designe tre trenger du en overordnet node og ulike undernoder. For å designe en graf, trenger du kryss og kant. Kant er et par hjørner.
Ovennevnte diskusjon konkluderer med at tre og graf er de mest populære datastrukturene som brukes til å løse ulike komplekse problemer. Grafer er en mer populær datastruktur som brukes i datamaskindesign, fysiske strukturer og ingeniørvitenskap. De fleste av oppgavene er utformet ved hjelp av grafdatastruktur. Korteste avstandsproblem er den mest brukte datastrukturen. I dette problemet må vi beregne den korteste avstanden mellom to hjørner.
Videre lesing:
- Forskjell mellom graf og tre



