Forskjell mellom parallellogram og trapesform: parallellogram vs trapesformet (trapesium)
Parallelogram vs Trapezoid
Parallelogram og trapes (eller trapes) er to konvekse firkanter. Selv om disse er firkanter, varierer geometrien av trapesen betydelig fra parallellogrammer.
Parallelogram
Parallelogram kan defineres som den geometriske figuren med fire sider, med motsatte sider parallelle med hverandre. Nærmere bestemt er det en firkant med to par parallelle sider. Denne parallelle naturen gir mange geometriske egenskaper til parallellogrammer.

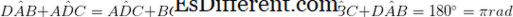
En firkant er et parallellogram hvis følgende geometriske egenskaper er funnet.
• To par motstående sider er like lange. (AB = DC, AD = BC)
• To par motstående vinkler er like store. (

• Hvis de tilstøtende vinklene er ekstra

• Et par sider som står mot hverandre, er parallelle og like lange. (AB = DC & ABidelDC)
• Diagonalene bisecter hverandre (AO = OC, BO = OD)
• Hver diagonal deler firkanten i to kongruente trekanter. (ΔADB ≡ ΔBCD, ΔABC ≡ ΔADC)
Videre er summen av sidens firkanter lik summen av firkantene av diagonaler. Dette er noen ganger referert til som parallellogram loven og har utbredt søknader i fysikk og ingeniørfag. (AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + BD 2 )
Hver av de ovennevnte egenskapene kan brukes som egenskaper, når det er oppdaget at firkanten er et parallellogram.
Parallellogrammets område kan beregnes med produktet av lengden på den ene siden og høyden til motsatt side. Derfor kan området for parallellogrammet angis som
Område med parallellogram = basis × høyde = AB × h
Parallellogrammets område er uavhengig av formen til det enkelte parallellogram. Det er kun avhengig av lengden på basen og den vinkelrette høyden.
Hvis sidene av et parallellogram kan representeres av to vektorer, kan området oppnås med størrelsen på vektorproduktet (kryssprodukt) av de to tilstøtende vektorer.
Hvis sider AB og AD er representert av vektorene (


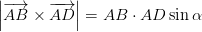


• Området til et parallellogram er dobbelt så stort som en trekant skapt av noen av dens diagonaler.
• Parallellogrammet er delt i halvdel av en hvilken som helst linje som går gjennom midtpunktet.
• En ikke-degenerert affine-transformasjon tar et parallellogram til et annet parallellogram.
• Et parallellogram har rotasjonssymmetri i rekkefølge 2
• Summen av avstandene fra et innvendig punkt til et parallellogram til sidene er uavhengig av Plasseringen av punktet
Trapesformet
Trapesformet (eller
Trapezium i britisk engelsk) er en konveks firkantet hvor minst to sider er parallelle og ulik i lengden. De parallelle sider av trapesformen er kjent som basene og de andre to sidene kalles bena. Følgende er hovedkarakteristikker av trapeser;

• Hvis de tilstøtende vinklene ikke befinner seg på samme basis av trapesen, er de tilleggsvinkler. Jeg. e. De legger opp til 180 ° ()

Begge diagonaler av et trapezium krysser i samme forhold (forholdet mellom delene av diagonalene er like). •
Hvis a og b er baser og c, d er ben, er lengdene på diagonalene gitt ved og
Arealet av trapesformet kan beregnes ved å bruke følgende formel
Areal av trapezoid =
Hva er forskjellen mellom Parallelogram og Trapezium (Trapes)?

•
Både parallellogram og trapesformet er konvekse firkanter. •
I et parallellogram er begge par av motstående sider parallelle, mens i et trapesformet, er bare et par parallelle. •
Parallellogrammets diagonaler halverer hverandre (1: 1-forhold) mens trapesformens diagonaler krysser med et konstant forhold mellom seksjonene. •
Parallellogrammet er avhengig av høyden og basen mens trapesens område er avhengig av høyden og midtsegmentet. •
De to trekanter som dannes av en diagonal i et parallellogram, er alltid kongruente, mens trekantene av trapesen kan enten være kongruente eller ikke.





