Forskjell mellom derivat og differensial

Derivative vs Differential

I differensialkalkulator er derivat og differensial av en funksjon nært beslektet, men har svært forskjellige betydninger, og pleide å representere to viktige matematiske objekter relatert til differerierbare funksjoner.

Hva er derivat?

Derivat av en funksjon måler hastigheten der funksjonsverdien endres når dens inngangsendringer endres. I multi-variable funksjoner avhenger endringen i funksjonsverdien av retningen for endringen av verdiene for de uavhengige variablene. Derfor er i slike tilfeller valgt en bestemt retning, og funksjonen er differensiert i den bestemte retning. Det derivatet kalles retningsbestemt derivat. Delvis derivater er en spesiell type retningsderivater.

Derivat av en vektorverdig funksjon f kan defineres som grensen

hvor den eksisterer endelig. Som nevnt før gir dette oss økningsraten for funksjonen f langs vektoren u. Når det gjelder en enkeltverdig funksjon, reduseres dette til den velkjente definisjonen av derivatet,

For eksempel er

overalt forskjellig, og derivatet er lik grensen,

, som er lik

. Derivatene av funksjoner som

finnes overalt. De er henholdsvis lik funksjonene

Dette er kjent som det første derivatet. Vanligvis er det første derivatet av funksjonen f betegnet ved f ⁽¹⁾ . Nå bruker du denne notasjonen, er det mulig å definere høyere rekkefølgenderivater.

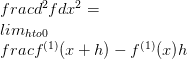
er den andre ordens retningsderivat, og betegner n ^th derivatet ved f ⁽ⁿ⁾ for hver n,

, definerer n ^th derivatet.

Hva er forskjell?

Differensial av en funksjon representerer endringen i funksjonen med hensyn til endringer i den uavhengige variabelen eller variablene. I den vanlige notasjonen er den totale differansen av rekkefølge 1 df gitt av for en gitt funksjon f av en enkelt variabel x

. Dette betyr at for en uendelig endring i x (dvs. d x), vil det være en f ⁽¹⁾ (x <) d x endring i f. Ved hjelp av grenser kan man ende opp med denne definisjonen som følger. Anta at Δ

x er endringen i x på et vilkårlig punkt x og Δ f er den tilsvarende endringen i funksjonen f. Det kan vises at Δ f = f (1) ⁽ x) A x + e, hvor e er feilen. Nå er grensen Δ x → 0 Δ ^{f /} Δ _{x =} f (1) ( ^x ) (med den tidligere angitte definisjonen av derivat) og dermed, Δ x → 0 e / ^A x = 0.Derfor er det mulig å konkludere med at Δ _{x → 0} ε = 0. Nå, betegner Δ x → 0 Δ f som d f og Δ x → 0A x som d x er definisjonen av differensialen strenge oppnådd. For eksempel er differansen av funksjonen.

Ved funksjon av to eller flere variabler defineres total differensial av en funksjon som summen av differensialene i retningene for hver av de uavhengige variablene. Matematisk kan det angis som

Hva er forskjellen mellom derivat og differensial?

• Derivat refererer til en forandringshastighet av en funksjon, mens differensialet refererer til den faktiske endringen av funksjonen, når den uavhengige variabelen blir endret.

• Derivatet er gitt ved

, men differensialet er gitt av

Forskjell mellom derivat og differensial

Anbefalt