Forskjell mellom definite og indefinite integraler Forskjellen mellom
Kalkulator er en viktig del av matematikk, og differensiering spiller en kritisk rolle i beregningen. Den inverse prosessen av differensieringen er kjent som integrasjon, og den inverse er kjent som integralet, eller ganske enkelt sett, gir inversen av differensiering en integrering. Basert på resultatene de produserer integralene er delt inn i to klasser, f.eks., bestemte og ubestemte integraler.
Definitivt integrert
- 9 ->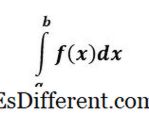
Det definerte integralet av f (x) er et tall og representerer arealet under kurven f (x) fra x = a i x = b .
En bestemt integral har øvre og nedre grenser på integralene, og det kalles definitivt fordi vi ved slutten av problemet har et nummer - det er et klart svar.
Ubestemt Integral

Den ubestemte integral av f (x) er en FUNKSJON og svarer på spørsmålet "Hvilken funksjon når differensiert gir f (x) ? "
Med en ubestemt integrering er det ingen øvre og nedre grenser på integralet her, og det vi får er et svar som fortsatt har x i det og vil også ha en konstant (vanligvis betegnet C ) i den.
Ubestemt integral gir vanligvis en generell løsning på differensialligningen.
Ubestemt integral er mer en generell form for integrasjon, og den kan tolkes som anti-derivatet av den vurderte funksjonen.
Anta at differensiering av funksjonen F fører til en annen funksjon f , og integrasjonen av f gir integralet. Symbolisk er dette skrevet som
F (x) = ∫ƒ (x) dx
eller
F = ∫ƒ dx
hvor både F og ƒ < er funksjoner på x , og F er differensierbar. I ovennevnte form kalles det en Reimann-integral, og den resulterende funksjonen følger med en vilkårlig konstant. En ubestemt integral produserer ofte en familie av funksjoner; Derfor er integralet ubestemt.
Integraller og integrasjonsprosesser er sentrale i å løse differensialligninger. I motsetning til trinnene i differensiering følger trinnene i integrasjon imidlertid ikke alltid en klar og standard rutine. Av og til ser vi at løsningen ikke kan uttrykkes eksplisitt når det gjelder elementær funksjon. I så fall er den analytiske løsningen ofte gitt i form av en ubestemt integral.
Den grunnleggende teorem for beregningen
Den definitive og det ubestemte integralet er koblet sammen med grunnleggende teorem for beregningen som følger: For å beregne en
definert integral , finn ubestemt integral > (også kjent som anti-derivatet) av funksjonen og evaluere ved endepunktene x = a og x = b . Forskjellen mellom bestemte og ubestemte integraler vil være tydelig når vi vurderer integralene for samme funksjon. Vurder følgende integral:
OK. La oss gjøre begge og se forskjellen.
For integrasjon må vi legge til en til indeksen som fører oss til følgende uttrykk:

På dette tidspunktet er
C
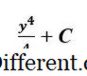
bare en konstant for oss. Ytterligere informasjon er nødvendig i problemet for å bestemme nøyaktig verdien av C . La oss evaluere det samme integralet i sin bestemte form i. e., med øvre og nedre grenser inkludert. Grafisk sett beregner vi nå området under kurven
f (x) = y

3 mellom y = 2 og y = 3 >. Det første trinnet i denne evalueringen er det samme som den ubestemte integrale evalueringen. Den eneste forskjellen er at denne gangen legger vi ikke til konstanten C .
Uttrykket i dette tilfellet ser ut som følger: Dette er sving fører til: I hovedsak erstattet vi 3 og deretter 2 i uttrykket og oppnådde forskjellen mellom dem.
Dette er den definitive verdien i motsetning til bruken av konstant

C

tidligere.
La oss undersøke den konstante faktoren (med hensyn til ubestemt integral) i noe mer detaljert. Hvis differansen på y
3
er 3y 2 , så ∫ 3y 2
dy = y 3 Men 3y 2
kan være forskjellen mellom mange uttrykk, hvorav noen inkluderer y 3 -5 , > y 3 +7 , etc … Dette innebærer at reverseringen ikke er unik siden konstanten er uklart for under operasjonen. Så generelt er 3y 2 differensialet av
y 3 + C hvor C er en hvilken som helst konstant. For øvrig er C kjent som 'konstant for integrasjon' . Vi skriver dette som: ∫ 3y 2
. dx = y
3 + C Integrasjonsteknikker for en ubestemt integrering, for eksempel tabelloppslag eller Risch-integrering, kan legge til nye diskontinuiteter under integrasjonsprosessen. Disse nye diskontinuiteter oppstår fordi anti-derivatene kan kreve innføring av komplekse logaritmer. Komplekse logaritmer har en hoppefrekvens når argumentet krysser den negative reelle aksen, og integrasjonsalgoritmene kan noen ganger ikke finne en representasjon der disse hoppene avbrytes.



